La fisica del cucchiaio di Pirlo.

Sicuramente molti di noi hanno ancora impresso lo splendido gol di Pirlo nella partita Inghilterra-Italia dei quarti di finale degli Europei di Calcio 2012. Ebbene si, è stato proprio un tocco da maestro! Ma dal momento che del gesto tecnico in quanto tale ne hanno già parlato abbastanza un po’ in tutti i giornali, essendo thegravityroom un blog di divulgazione scientifica sia specialistica che di ampio respiro, quello che volevo fare in questo post è appunto concentrarmi sulla fisica di questo fenomeno. Di che fenomeno si tratta innanzitutto? Il fenomeno che un po’ tutti conosciamo è quello di una palla che avanza con una “lentezza” inusuale, accompagnata da una strana traiettoria. La causa che sta dietro a questo comportamento è un effetto che agisce sulla palla denominato effetto Magnus.



L'effetto Magnus, scoperto da Heinrich Gustav Magnus (1802-1870), è un caso particolare del principio di Bernoulli che cita così: in un fluido ideale su cui non viene applicato un lavoro, per ogni incremento della velocità si ha simultaneamente una diminuzione della pressione o un cambiamento dell'energia potenziale gravitazionale del fluido. 

Matematicamente questo si esprime con: \[p+\rho\frac{v^{2}}{2}+\rho gh=costante\] Dove v rappresenta la velocità del fluido lungo la linea di flusso, g l'accelerazione di gravità, h è l'altezza rispetto ad un riferimento orizzontale, p rappresenta la pressione lungo la linea di flusso e ρ è la densità del fluido. Questa equazione, sotto alcune approssimazioni, spiega il motivo per il quale gli aerei riescano a volare. Il segreto sta tutto nella forma delle ali che sono costruite in modo da rendere la velocità dell'aria sulla faccia superiore maggiore di quella sulla faccia inferiore. Questa tecnica permette di generare una forza diretta verso l'alto, chiamata portanza, data da una pressione sulla faccia inferiore maggiore di quella sulla faccia superiore. Dall’equazione di Bernoulli abbiamo che: \[p_{i}+\rho\frac{v_{i}^{2}}{2}=p_{s}+\rho\frac{v_{s}^{2}}{2}\] Dove p è la pressione dell'aria sulla faccia inferiore (i) o superiore (s), a seconda del pedice, e v la velocità dell'aria sulla faccia inferiore o superiore. Quindi la differenza di pressione che agisce sull’ala è: \[P = \left(p_{i}-p_{s}\right)=\rho\frac{v_{s}^{2}}{2}-\rho\frac{v_{i}^{2}}{2}\] Questa differenza di pressione P=(pi-ps) si manifesta come una forza direttamente proporzionale alla superficie inferiore dell'ala. Infatti dalla definizione di pressione come rapporto tra la forza (F) agente perpendicolarmente alla superficie (S) e la superficie stessa, P=F/S, ne consegue che la forza sarà F=P*S. 

A causa del differente percorso che l'aria è costretta a seguire nella parte superiore e nella parte inferiore dell'ala, dovuto alla diversa curvatura delle due superfici, si determina una velocità maggiore delle linee di flusso superiori rispetto a quelle inferiori affinché esse si possano ricongiungere nello stesso istante. Per la legge di Bernoulli ad un incremento di velocità corrisponde una diminuzione della pressione, con una conseguente forza F (portanza) diretta verso l’alto.

L’effetto Magnus responsabile del pallone a cucchiaio e dei più generali “tiri ad effetto” ha una spiegazione molto simile. Infatti, se attorno alla palla vengono a crearsi due zone, una nella quale l’aria scorre più velocemente e un’altra, dal lato opposto, in cui l’aria scorre più lentamente, la situazione sarà analoga al caso del profilo alare in cui nella superficie inferiore la velocità del flusso d’aria è minore rispetto alla velocità del flusso d’aria nella superficie superiore, generando una forza che spinge l’ala verso l’alto. 

Ma perché mai con un pallone dovrebbe venire a crearsi questa curiosa situazione? 

La risposta è semplice: ciò avviene se la palla è messa in rotazione. Se il corpo infatti ha un moto di traslazione rettilinea è come se venisse investito da una corrente di fluido che si muove in direzione opposta a quella del corpo. Tuttavia, se il moto è puramente di traslazione rettilinea (senza rotazione per capirci) le linee di corrente saranno ugualmente spaziate tra loro intorno al corpo, indice del fatto che la velocità del fluido sopra e sotto è uguale, con il risultato che nessuna forza netta agisce sulla palla (a parte l’attrito che tenderà a rallentare la stessa). Nel momento in cui la palla è dotata di moto sia rotatorio che traslatorio, la velocità del fluido aumenta superiormente o inferiormente alla palla stessa a seconda del suo verso di rotazione. Questo avviene proprio per il trascinamento del fluido attorno al corpo stesso. Prendiamo come esempio la situazione nella figura sottostante, in cui la palla si muove da destra verso sinistra, con una certa velocità del baricentro, ruotando allo stesso tempo in senso retrogrado, cioè la palla ruota con il verso opposto alla direzione del moto. Nel sistema di riferimento del baricentro della palla, la velocità rotazionale del punto superiore, denotato con la lettera S, è in senso concorde alla velocità dell’aria (nel sistema di riferimento del baricentro è l’aria che si muove con la velocità della palla stessa, ma in direzione opposta), con il risultato di un trascinamento maggiore del primo strato d’aria a contatto con la palla rispetto al punto inferiore, i, in cui la velocità rotazionale della palla è in senso discorde rispetto alla velocità dell’aria. Dal momento che l’aria è un fluido viscoso, il trascinamento del primo strato è comunicato agli strati adiacenti, con l’effetto di addensare le linee di flusso con una velocità dell’aria maggiore negli strati superiori alla palla piuttosto che in quelli inferiori (Vs>Vi). Per la legge di Bernoulli a un incremento di velocità corrisponde una diminuzione della pressione, con una conseguente forza F diretta verso l’alto, perpendicolarmente al moto della palla stessa.

Effetto Magnus dovuto alla rotazione della palla, visto nel
sistema di riferimento del baricentro della stessa.

Se ora ripensiamo al calcio di rigore ad opera di Pirlo siamo in grado di capire il motivo per il quale il pallone subisca quella strana traiettoria e spiegare perché la palla sembra essere “al rallentatore”. Sembra infatti che il moto sia compiuto in un tempo maggiore di quello che uno si aspetta; anche questo è dovuto al fatto che se la palla è posta in rotazione retrograda durante il volo la gittata è più lunga rispetto a quella attesa*, dal momento che il tempo in funzione della gittata è espresso dalla legge: \[t=\frac{x_{G}}{v_{0}\cos\theta}\] a parità di velocità iniziale, V0, e di angolo di lancio, θ, il tempo risulta più lungo se la gittata, XG, è maggiore. 
Quindi abbiamo compreso in parte qual è il segreto che sta dietro i tiri ad effetto. 

Riassumendo, quali sono gli ingredienti principali per un ottimo “tiro a cucchiaio”? 

1. La rotazione: la palla deve essere messa in rotazione, infatti il tiro “a cucchiaio” è così chiamato perché ricorda il movimento a scavare che si fa con questo tipo di posata. Questo movimento è necessario se si vuole colpire la palla “strisciandola” dall’alto verso il basso in modo da impartirle una rotazione in senso opposto al movimento netto della palla verso la porta. 
2. Un mezzo: è importante che vi sia un mezzo in cui la palla scorra, nel nostro caso è l’aria che, a causa della diversa velocità di scorrimento rispetto a diverse parti del pallone, produce una forza netta su di esso, dovuta all’effetto Magnus, che gli fa compiere “strane” traiettorie. 
3. La gravità: nel caso del gioco del calcio serve anche una forza diretto verso il basso come la gravità, questo non perché altrimenti l’effetto Magnus verrebbe a mancare, ma per permettere alla palla di riscendere una volta lanciata. 
4. Il talento: non ultimo serve un giocatore di talento, ma soprattutto impavido, che sappia realizzare un tiro di cotanta maestria e sebbene uno possa conoscere in dettaglio le leggi che governano il movimento dei corpi nei mezzi fluidi, non è detto che sia anche in grado di saper sfruttare queste leggi di natura. Per cui, se non vi chiamate Andre Pirlo, Francesco Totti o Antonìn Panenka**, potete o allenarvi  più duramente a calcio oppure studiare la FISICA  e le leggi che governano la natura perché almeno vi potete consolare affermando: ”io so spiegare il motivo per cui il cucchiaio funziona proprio così!!”. 


Curiosità: 
- La palla usata nei mondiali di calcio del 2010 è stata criticata per avere un diverso effetto Magnus rispetto alle palle usate nelle competizioni precedenti. Questo è dovuto alla diversa rugosità della sfera, determinante per generare il trascinamento degli strati d’aria. 
- Altre tipologie di tiri ad effetto: il tiro a “Foglia morta” è un calcio di punizione diretto calciato sopra la barriera facendo compiere al pallone una traiettoria pressoché lineare in fase ascendente e ad effetto in fase discendente. Si effettua con l'interno del piede, quasi senza rincorsa e senza eccessiva potenza. Il termine fu coniato per le punizioni di Mario Corso.
-Andrea Pirlo nel 2005 ha aggiunto al suo bagaglio tecnico anche una nuova modalità di tiro ad effetto: "l'ascensore” (nome coniato dai suoi compagni di squadra) ispirandosi a Juninho Pernambucano.
_________________________________________________________________

UPDATE: Mondiali di Calcio 2014

Dal momento che sono in atto i mondiali di Calcio in Brasile mi sembrava doveroso aggiornarvi sulla "fisica nei campi da calcio". Proprio ieri, nel corso della partita Italia-Inghilterra, è arrivata una dimostrazione di come la traiettoria di un pallone possa essere imprevedibile a causa degli effetti legati alla rotazione dello stesso (e non solo). Qui sotto potete rivedere voi stessi la bizzarra traiettoria del calcio di punizione: la palla colpisce la traversa e il portiere inglese, Hart, è totalmente spiazzato.  

E in ultimo la reazione del portiere dell'Inghilterra all'incontro con Andrea Pirlo, si congratula con un "WOW", che dice tutto su quanto fosse sorpreso.  

Una nota di servizio: una simile traiettoria non è dovuta agli effetti imprevedibili dell'odiatissimo Jabulani, ricordate? Il pallone ufficiale dei mondiali di calcio del 2010, che non piaceva soprattutto ai portieri proprio perché assumeva delle traiettorie imprevedibili. 
Il nuovo pallone in dotazione per questa edizione dei mondiali, il Brazuca, invece pare avere delle traiettorie più stabili. A confermarlo sono i test aerodinamici eseguiti dalla NASA,  di cui sotto potete vedere alcune immagini e il video.

Il punto chiave è la velocità a cui viene a crearsi una situazione di forte instabilità nell'aria dietro e attorno il pallone (rispetto alla direzione di moto). E' cioè quello che in fisica viene definito il numero di Raynolds critico, il valore cioè del numero di Raynolds in corrispondenza del quale si ha il passaggio tra il regime laminare e il regime turbolento. 

Regime laminare.

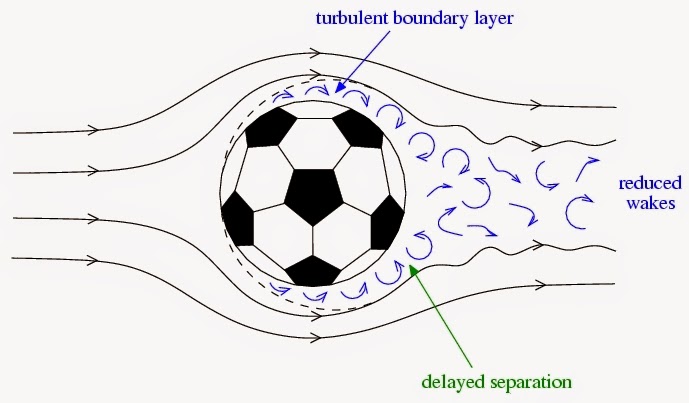Formazione del regime turbolento.

Quando sia ha questa transizione tra regime laminare e turbolento, che dipende dalla velocità del pallone, la traiettoria dello stesso diventa imprevedibile proprio a causa delle turbolenze dell'aria che condizionano la traiettoria della palla in maniera non lineare. 

Ebbene gli studi condotti dalla NASA hanno dimostrato che la velocità critica a cui si ha questa transizione, utilizzando il pallone Jabulani, è di circa 80 km/h, mentre per i palloni tradizionali questa velocità è di circa 42 km/h. 

Il fatto che la velocità critica dello Jabulani sia di circa 80 km/h, che è una velocità tipica per i traversoni e/o i tiri in porta, così come le punizioni di un giocatore medio, ha fatto si che la natura imprevedibile della traiettoria del pallone si manifestasse più frequentemente durante i precedenti mondiali e che si manifestasse proprio nei momenti più decisi di una partita: durante i tiri verso la porta. 

Ma quale è quindi la differenza del nuovo Brazuca? 

Dal momento che la transizione tra regime laminare e turbolento dipende, tra le altre cose, dalla rugosità del pallone, il Brazuca è stato reso più ruvido del suo cugino Jabulani che invece presentava una superficie leggermente più liscia. 

Superficie rugosa del nuovo pallone dei mondiali di calcio 2014,
il cosiddetto Brazuca.

La differente rugosità ha un effetto drastico sulla velocità critica a cui appare il regime turbolento, che per il Brazuca infatti scende a soli 42 km/h. Ci si aspetta che la traiettoria di quest'ultimo sia molto più prevedibile e stabile, soprattutto nei momenti decisivi come nei calci di punizione e nei tiri in porta in generale. 

Per concludere quindi la bizzarra traiettoria seguita dalla palla nella punizione di Pirlo contro l'Inghilterra non è merito della palla ma del talento del calciatore ;) 

Ai prossimi aggiornamenti :)

_______________________________________________________________________________

 *Tra l’altro è il motivo che condusse Peter Tait, matematico scozzese grande appassionato di golf, a studiare tale effetto. Egli notò che quando la pallina da golf veniva colpita in modo da metterla in rotazione retrograda, la gittata era più lunga rispetto a quella attesa. 

**1976, Belgrado, finale degli Europei di calcio tra Cecoslovacchia e Germania Ovest : la partita finisce sul 2-2 e dopo i tempi supplementari si va ai calci di rigore. La Cecoslovacchia realizza i primi quattro tiri dal dischetto, mentre il tedesco Hoeness sbaglia il quarto rigore della Germania. Per il calcio di rigore decisivo va sul dischetto il centrocampista cecoslovacco Antonìn Panenka, l'eventuale gol porterebbe la Cecoslovacchia a vincere per la prima volta la competizione Europea. Panenka, porterà la Cecoslovacchia al successo battendo il portiere tedesco Sepp Maier, calciando per la prima volta nella storia del calcio un originale e inusuale tiro che fu denominato con l’ormai famoso nome di “tiro a cucchiaio”.